大师访谈之如何看懂方差齐性检验结果

大师访谈之如何看懂方差齐性检验结果

方差齐性检验是数理统计学中检验不同样本的总体方差是否相同的一种方法。方差齐性的结果会影响后续统计分析方法的选择。因此在数据分析和变量比较前, 进行方差齐性检验是很有必要的。方差齐性检验在医学统计中也十分常见。例如在ADA研究中，方差齐性检验是病人群体能否沿用健康人群阈值的关键之一。

方差齐性检验常用的方法有F test和Levene’s test 等。 本期文章采访了两位统计大师，他们分别是Snedecor教授和Levene教授，两位大师的介绍如下：

由于不可抗力因素，无法与两位教授面谈，故在今年清明节采用线上采访形式与两位大师联系（内附绝密聊天记录！！！别问，问就是被关疯了…）。

绝密聊天记录如下：

绝密文件1：

例如我们比较下表中的两组数据：

表格 1示例 不同人群数据

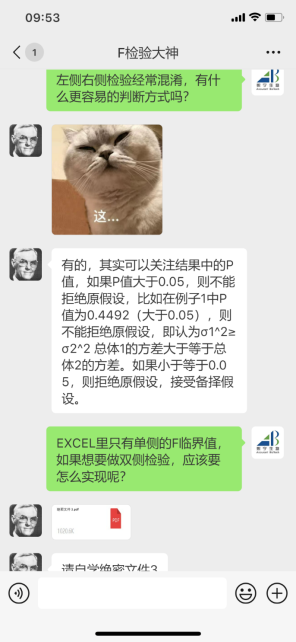
选取变量1为总体1，变量2为总体2，然后用EXCEL实施F检验，结果如下：

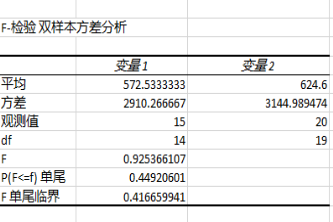
图 1  EXCEL F test左侧检验结果

首先观察到变量1的方差(2910.266667)小于变量2的方差(3144.989474)（即）。由样本推断总体，我们可以假设总体1的方差也会小于总体2的方差，所以原假设（H0）就是 ，备择假设（H1 or Ha）为，因此：

由备择假设（Ha or H1）可知，该检验为左侧检验。所以该检验的拒绝域（拒绝原假设的区域）为下图阴影部分：

图 2左侧检验拒绝域

选取，图中的。因此如果计算出来的F值（0.925）落在拒绝域中(F小于)则拒绝H0，即认为总体1的方差会小于总体2的方差。在这个例子中F值（0.925）大于，没有落在拒绝域中，所以不能拒绝原假设，因此认为总体1的方差大于等于总体2的方差。

绝密文件2：

假设还是上述两组数据，这次选取变量1为总体2，变量2为总体1，然后用EXCEL实施F检验，结果如下：

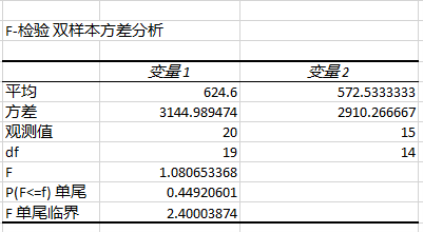
图 3 EXCEL F test 右侧检验结果

• 首先观察到变量1的方差(3144.989474)大于变量2的方差(2910.266667)（即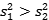）。由样本推断总体，我们可以假设变量1总体的方差也会大于变量2总体的方差，所以原假设（H0）就是 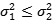，备择假设（H1 or Ha）为，因此：

可以发现此F值（1.080653368是例1中F值（0.9253661）的倒数），由备择假设（Ha or H1）可知，该检验为右侧检验。所以该检验的拒绝域（拒绝原假设的区域）为下图阴影部分：

图 4右侧检验拒绝域

选取，图中的。因此如果计算出来的F值（1.081）落在拒绝域中(F大于)则拒绝H0，即认为变量1总体的方差会大于变量2总体的方差。在这个例子中F值（1.081）小于，没有落在拒绝域中，所以不能拒绝原假设，因此认为变量1总体的方差小于等于变量2总体的方差。但是在这个例子中，变量1代表的是总体2，变量2代表的是总体1，所以结论是总体2的数据的方差小于等于总体1数据的方差，该结论与例子1一致。

因此在用EXCEL做分析时，不论是先选择哪组人群，得到的结论是一致的，重要的是分清左侧检验还是右侧检验。

绝密文件3：

双侧检验的原假设（H0）是，备择假设（H1 or Ha）是。双侧检验的拒绝域如下：

图 5 双侧检验拒绝域

在EXCEL中实施时，由于是双侧检验，所以在EXCEL设置时，需要将设置成，例1中的，因此换成双侧检验后需设置，结果如下：

图 6 EXCEL F test双侧检验结果

同理，我们也可以关注P值得出结论，因为是双侧，所以需要将结果中单尾的P值乘以2（），然后将双侧P值与0.05比较，如果大于0.05则不能拒绝原假设。在这个例子中双侧的P值为0.8984大于0.05，所以不能拒绝原假设，即认为，两组人群的方差相同。如果得出的P值小于等于0.05，则拒绝原假设，认为两组人群的方差不同。

趁热打铁，我来连线一下Levene教授，借借清明节的东风。

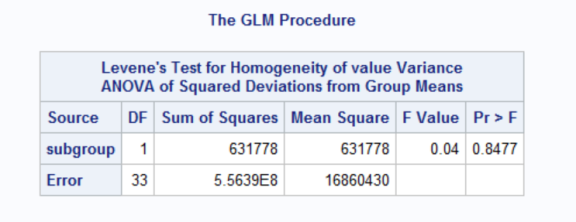
图 7 Levene's test 结果

小结：

F检验和Levene’s检验都可以用来对比不同组的方差，但是F检验对正态数据十分敏感，所以适合使用的情况有限。在EXCEL中实施F检验时，需要关注研究问题是单侧检验还是双侧检验，解读结果时，可以通过比较P值(双侧检验取的是2倍的P值)和0.05来得出结论。Levene’s 检验既可用于正态数据也可用于非正态数据，所以被广泛认为是比较方差齐性的标准方法之一，也被推荐为ADA研究中检验健康人群与病人群体方差是否齐性的方法。

以上情节纯属虚构,不会有雷同。

参考文献：

1.       Recommendations for Systematic Statistical Computation of Immunogenicity Cut Points

2.       F-tests for Equality of Two Variances (saylordotorg.github.io)

3.       F-Distribution Tables (ucla.edu)

4.       Levene's test - Wikipedia

5.       SAS Help Center: Example 48.10 Testing for Equal Group Variances